Optimising the 2048 Game Engine

The goal of this project was to produce a highly optimised engine for the game 2048. The game engine implements all the behaviour needed to play the game 2048, such as shifting and merging tiles, inserting random new tiles, and calculating the score. My MSc thesis was on using artificial intelligence methods to find strategies for the game of 2048. The aim was to find strategies which human players could understand and replicate whilst maximising performance. This required testing millions of possible strategies, making billions of moves. Therefore, having a fast game engine was an essential foundation. To stress test the engine an expectimax algorithm was used. This algorithm can perform very well on 2048, often reaching the 32,768 tile. To achieve a score so large, more than 18,000 moves and over 90 billion game states need to be considered. If the engine was not extremely well optimised this would take a very long time.

In this post I discuss the following:

Methodology used to create the optimised engine
Implementation details of the engine
The expectimax algorithm

The engine implemented takes roughly 3 nanoseconds to make a move, a factor of 30,000 faster than the 100,000 nanoseconds that the original web version. The expectimax algorithm uses heuristics developed in previous work, but takes advantage of multithreading to run over 50% faster.

The game below is an adapted version of the original [1]. It is being played by the expectimax algorithm with a search depth limit of 6. The code for the engine, expectimax algorithm and WebAssembly interface can be found here [2].

Why Rust?

As performance of the engine was essential it was important that the language used to develop the engine did not introduce significant overhead. Rust was ideal as it has no runtime or garbage collector, resulting in performance characteristics similar to C/C++. Rust also has excellent support for WebAssembly [3], allowing the optimised engine code to be run in the browser. As the goal of the thesis was to try and find strategies a human could understand user tests were carried out, these user tests were conducted using a site I developed [4]. Therefore, being able to use the optimised engine in the browser was essential. It also allowed me to run the expectimax algorithm in the browser as you can see being demonstrated above.

Methodology

1. Create a basic, unoptimised implementation of the engine along with a test suite.

The basic implementation acted as a starting point. It was a complete engine that fully captured the rules of the game. However, it was not designed with speed in mind. The engine was fast enough for a person or simple computer agents to play, but if left unoptimised would have been a significant barrier to developing algorithms that require more computation. The test suite ensured that the implementation fully captured the game rules. As the engine was optimised and the code changed this test suite provided a guarantee that no bugs were being introduced.

2. Research existing approaches to building AI for 2048. See what techniques they used to produce an optimised engine.

This research involved reading papers and posts online from people who were working on developing AIs to play 2048. Of particular interest was a post on Stack Overflow [5]. The final version of the optimised engine uses the techniques described to achieve a high level of performance.

3. Build an expectimax algorithm to play the game.

This algorithm can require the consideration of over 90 million game states for an individual move making it a good test for the performance of the engine.

4. Use the profiling tools on a run of the expectimax algorithm. Identify the bottlenecks.

Profiling tools were used to understand which areas of the code were taking the most time and acting as bottlenecks. The Linux tool ‘perf’ [6] was used to gather data. To visualise the data generated by ‘perf’ flame graphs were used [7]. This made it easy to identify the code that was taking the most time. One of the flame graphs produced can be seen in Figure 1.

Profiling the code required an executable that would stress test the engine. The expectimax algorithm developed was perfect for this, the large number of game state considered acts as a great wat to thorougly test the performance of the engine and gather data for profiling.

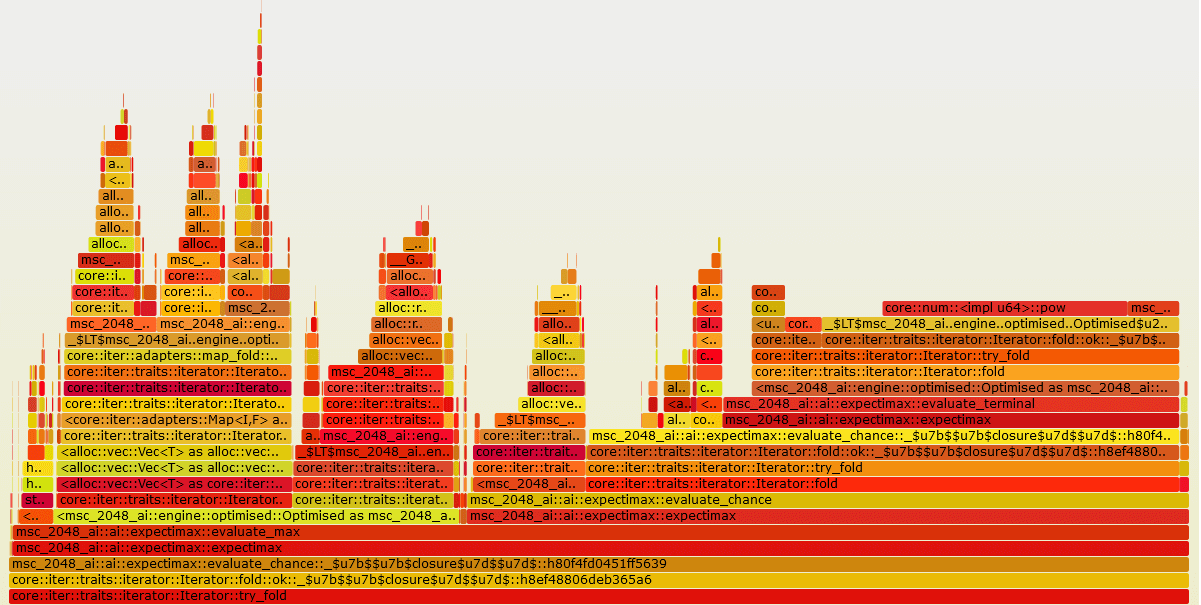
example flamegraph — Figure 1: Example of a flamegraph produced using the profiling tools.

5. Create benchmarks for the code identified using the profiling tools.

Benchmarks were used to measure the performance characteristics of the engine. The benchmarks were created using a library called Criterion [8]. Criterion stores data from previous benchmarks and uses them to compare to the current benchmark to show the changes in performance.

The data generated from running the profiling tools on the expectimax algorithm provided insights into what code was causing the bottlenecks in performance. If they did not already exist, benchmarks were created to cover the area of the code identified. The code was then changed in an attempt to make it have higher performance. After making changes the benchmarks were rerun to identify if the changes had improved the performance. If they had the changes would be kept. This process was repeated until there were no further changes to be made to improve the performance of the engine.

6. Edit the code to try to improve the performance.

Use algorithms and data structures found during research along with new ideas of how to improve performance. After making the changes rerun the benchmarks to ensure performance has improved. Steps 4-6 were repeated until no further performance improvements could be made.

Implementation

This implementation was based off the work done by Nneonneo [5]. The game state is represented using a single 64-bit integer. This integer is split into 16 4-bit chunks to represent each tile of the board. Each of these 4-bit chunks does not contain the true value of the tile on the board as it is only possible to represent the decimal numbers 0-15. Instead the number represents the exponent of the power of 2 required to get the true tile value. This allows tiles up to the value 32,768. The highest possible tile theoretically is 131,072. However, even the best AIs have never reached the tile of 65,536. The aim of this project was no to try to produce an AI that is the state of the art, as a result, the implementation does not handle cases where the tile is larger than 32,768. Bitwise operations are used to interact with the board state.

A cache is used to store all the possible shifts of the rows or columns: shift row left, shift row right, shift column up and shift column down. As each row/column can be represented using a 16-bit integer there are 65,536 different possibile states. When the engine is initialies the resulting value after shifting for each direction is calculated and the results are stored in an array of length 65,536. This means there is some initial overhead to generate the arrays, but after calculating shifts only requires an array lookup rather than a more complicated computation. There is also a cache that contains the resulting score for each row. For the use cases I am concerned about, which require consideration of a huge number of game states, this initial overhead to produce the cache is well worth it.

These optimisations to the engine mean that the computation for making a move can be carried out in 3 nanoseconds. Allowing consideration of billions of game states in a reasonable amount of time. The original web version takes rougly 100,000 nanoseconds per move. The optimisation resulted in engine that was faster by a factor of 30,000.

Expectimax

The expectimax algorithm is similar to the more popular minimax algorithm. In the minimax algorithm when deciding the best move to make one considers the best possible move of the opponent. In the expectimax algorithm the opponents options are weighted by the probability that the opponent will use that option. For 2048 the opponent can be considered to be the random tile additions to the board. Therefore, every empty tile location with both the 2 and 4 tiles are considered. The players options are of course the 4 move directions. The move the algorithm will recommend is the one which, after considering all the possibilites will most likely return the highest score. This score is not the score of the game state but is a heuristic score designed to encourage desirable game states. I did not make any adaptions to previous work [5]. Figure 2 shows an example of the start of the expectimax search tree if there are 3 empty tiles after shifting in any of the directions.

As the depth of the search tree increases the number of states that need to be considered grows exponentially. The search depth is incremented after considering both the move and the new tile location so Figure 2 is only at a search depth of 1 and already considers 29 different game states. The depth the expectimax algorithm will search is calculated as follows.

search_depth = max(3, number_of_unique_tiles - 2)

At this search depth it is possible for over 90 million different game states to be considered for an individual move. For games that reach the 32,768 tile more than 18,000 moves can be made and more than 90 billion game states considered. Note: the algorithm used on this site limits the search depth to a maximum of 6 to make it run faster, this does sacrifice performance but still regularly achieves the 16,384 tile.

The highly optimised rust engine along with the expectimax algortihm was as fast as the C++ implementation by Nneonneo [9]. As I used the same heuristics the score the algorithm can achieve was also the same. I improved the speed of the expectimax algorithm using multithreading. Each of the initial branches was evaluated in its own thread, making the algorithm run in 4 threads as opposed to 1. On my PC the multithreaded version would make a move in an average of 20ms compared to the 42ms of the single threaded version. The multithreaded version was therefore over 50% faster. As far as I am aware, this is the best performing expectimax algorithm for the game of 2048 created. As the expectimax algorithm is one of the best AIs created, the AI produced in this project is one of the best performing in the world! I expect that the search tree could be paralellized further, however I didn't want to spawn a new thread for every branch as I thought the overhead for thread creation would likely outweigh the benefits. I did not experiment with this as producing the fastest expectimax algorithm was not the goal of the project.

As the heuristics used were the same as those used by Nneonneo one would expect the distribution of highest tiles reached to be the same. Interestingly, after running the algorithm for 100 games the distribution was significantly different. The percentage of games that reached at least the 16,384 was similar, 92% compared to the 94% reported by Nneonneo [5]. However, in my 100 runs the 4096 tile was the highest tile once and the 32,768 tile was only reached in 22% of the games. The medians were similar with 393,178 compared to 387,222, interestingly that means even though the 32,768 tile was reached less the median score achieved was higher. The higest score reached was also higher during my 100 runs, with a score of 806,864 compared to 794,076. As the game is inherently very random there is a large variance in the results achieved, which is likely what caused the number of games in which the 32,768 tile to be significantly less. The 100 runs used is not enough to report an accurate highest tile distribution, meaning it is likely that both reported distriutions are inaccurate.

Statistic	My result	Nneonneo's result
Runs that reached at least 4096	100%	100%
Runs that reached at least 8192	99%	100%
Runs that reached at least 16384	92%	94%
Runs that reached at least 32768	22%	36%
Median score	393178	387222
Maximum score	806864	794076

Summary

The goal of this project was to produce a 2048 engine that could consider game states as fast as possible to facilitate the consideration of millions of different strategies as part of my master's thesis. An expectimax algorithm was developed to stress test the engine and profiling and benchmarking tools used to guide changes and ensure their efficacy. The resulting engine could make moves in approximately 3 nanoseconds, allowing billions of game states to be considered in a reasonable time. In addition, multithreading was used to improve the speed of the expectimax algorithms search by over 50%. The heuristics used were sourced from the best current expectimax implementation for 2048, meaning the expectimax algorithm here is the best performing created.